What Are Rep-4 Tiles in GeometryIn geometry, the notion of rep-tiles is one that fascinates a lot of people and who doesnt like classifying shapes as those which can be fragmented into smaller copies! A shape is said to be a rep-n tile if it can divided up into n of its copies. This determines, among other shapes like squares, rectangles and parallelograms and rhombuses whether every triangle is a rep-4 tile.
Rep-4 Tiles: What Are They & How Do You Define Them?
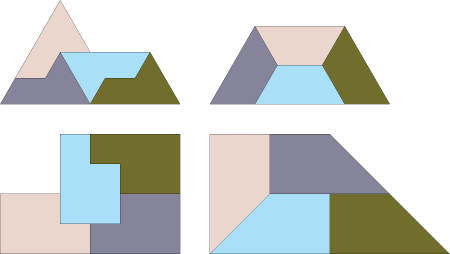
A rep-4 tile specifically denotes a shape that can fit together four smaller tiled copies of itself. For example, we know that every square (including the 1-tall by n-wide squares), rectangle.parallelogram,rhombus,and triangle is a rep-4 tile but those are just special cases(asside from triangles they can all also be regarded as varying degree kites). Effectively this means that they can be four times the same shape; through scaling and rotation,12 these shapes are dissectionally equivalent.
Examples of Rep-4 Tiles
Square : If is divided into 4 square smaller squares,
Rectangles: Rectangulars are forming by the same method like square; can be divided in 4 smaller rectangles.
Parallelograms: They keep properties under dissection and can be dissected into four smaller parallelograms
Triangles: Equilateral triangles can be partitioned into four smaller equilateral 30 tiles4, implying they are rep-4 on the list5.
Implications for Other Shapes
His concept is goes beyond mere polygons. Florida tiles by me, also based on rep-tiles next blog may we have an answer? The power to divide shapes into pieces of equal size results in their geometric properties, such as being applicable for tiling and using them within fractal designs.
Broader Mathematical Context
Rep-tile research lies at the nexus of tiling and fractals.rep-tile (ad) The Sierpinski triangle is an archetypal example of a fractal with (dis)canting properties, where individual motifs are rep-tile-dissected13. Cornering rep-tilenessOf course, knowing which shapes can and cannot play the role of a reptile raises questions on how this information may be geared for use in art and even architectural design or computer graphics.
So, the conclusion is: Prove that all triangles are rep-4 tiles (or not), but when you do so be sure to take some time with this neat theorem about centered hexagonal numbers!